It would come as no shock to anyone who knows me that my favorite christmas movie of all time is Home Alone.
It was during a rewatching of this movie the other night that I had the thought I’m sure most do, “How do Marv and Harry withstand this physical abuse?” Now, of course, it’s fiction so plot armor and the comedic punchlines protect Marv and Harry from straight up dying at the hands of Kevin. It would be an astoundingly less humorous movie if both wannabe criminals die or are knocked unconscious immediately when they slip on the ice outside the home.
This line of thinking, however, led me to a second question of “What were the physics of some of these injuries that Kevin was dealing out?” It was then that I decided to dust off some of my old textbooks and take a crack at answering this question and specifically with regards to the paint cans in the stairwell incident.
The first task in understanding the physics of the paint can incident is to reframe the mechanics as that of a pendulum. Kevin has tied two paint cans to the second floor bannister. The length of string between each paint can and the bannister is the pendulum arm length. Kevin has the paint cans balancing on the bannister but then pushes/lightly tosses them out. The paint cans don’t fall straight down. They swing pendulously.
An assumption that I made here is that the force Kevin uses to toss the paint cans is just enough to extend the pendulum to its full length. The paint cans have no kinetic energy before they begin their downward swing; only potential energy.
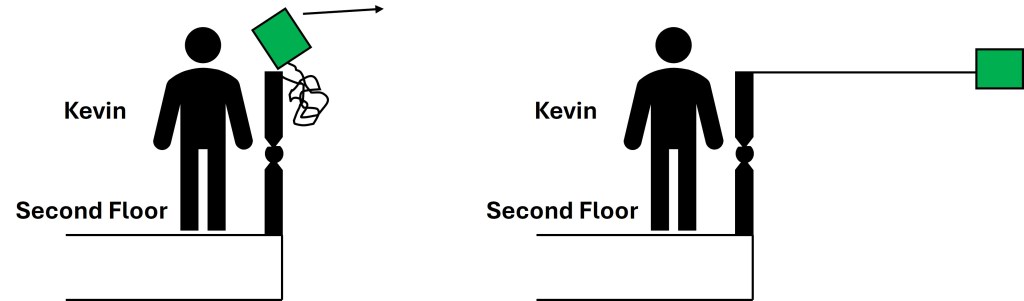
The assumption that the paint cans have no initial velocity right before they begin to swing down is to make it possible to calculate the velocity at which they impact Harry/Marv. If initial velocity isn’t assumed to be 0 the final velocity would be impossible to calculate.
The next step I undertook in this physics challenge was to determine the pendulum length. This was actually quite difficult. I watched the scene multiple times and paused it at key moments trying to count the steps on the staircase and the steps Harry has ascended before impact. Both Marv and Harry are impacted at approximately the same spot; although, Marv seems to have been hit when the paint can had swung slightly past its lowest point and thus with less velocity than the paint can that hit Harry. Harry’s location on the staircase is easier to determine (I say this despite going frame by frame for at least an hour) and seems to be on the fifth step. If you look at different stills for the movie online you can see that the portion of the stairs before the landing has thirteen steps with the thirteenth being the landing. The second portion of the staircase has only four steps with the fourth step being the second floor. This means that Harry would still have to climb 12 steps before reaching the top.
Given the above information the distance between Harry’s feet and the rotation point of the pendulum can be denoted as the following.
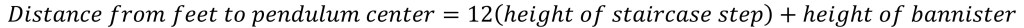
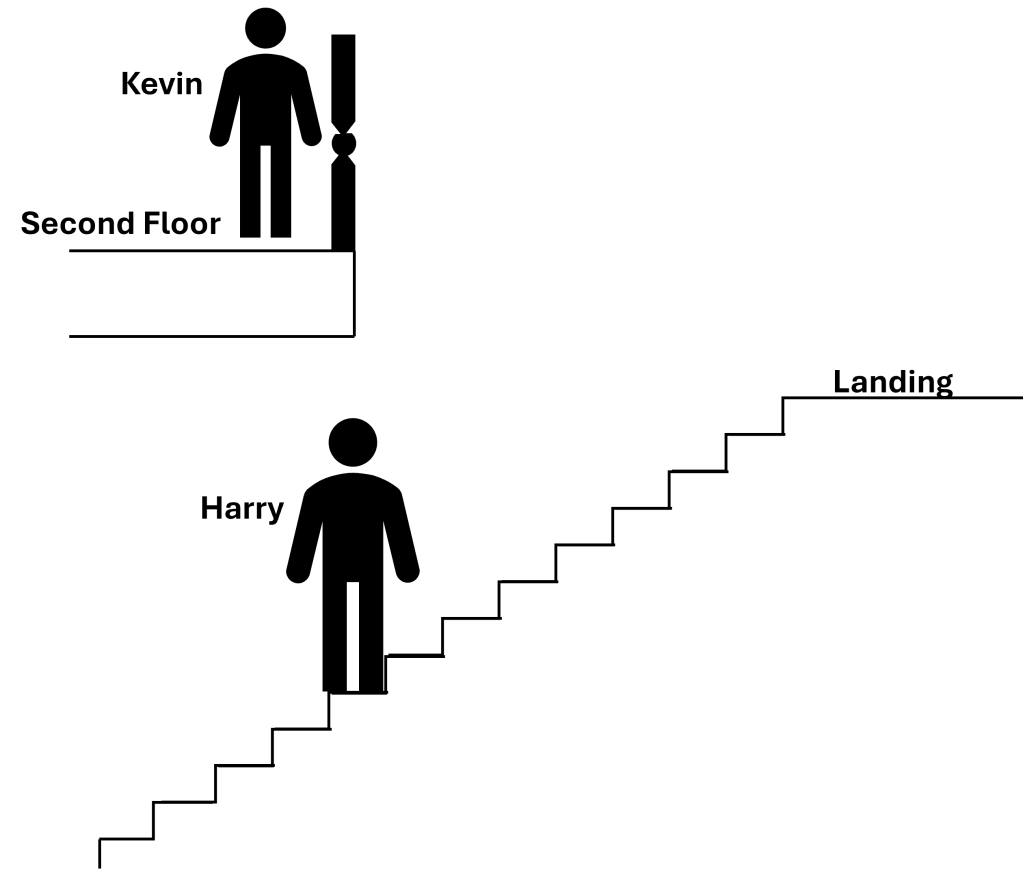
The paint can hits Harry in the forehead. If we subtract Joe Pesci’s height from above equation we should get close to the measurement of the pendulum arm. [One could argue that since the paint can hits Harry in the forehead subtracting Joe Pesci’s height will underestimate the pendulum arm length. However, in the film, Pesci is wearing shoes and the distance from the top of his head to where the can strikes and the height gained from shoes is likely comparable.]
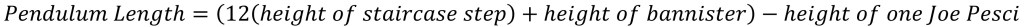
The layout of the stairs and the corresponding locations of Harry and Kevin are pictured in the following two images.

According to a quick Google search, the height of a staircase step can range from 6.25 – 7.875 inches. It is reasonable here to use the mean value of 7.06 inches. The Americans with Disabilities Act (ADA) states that bannisters should be between 34 and 38 inches in height. I didn’t do a deep dive into whether this applied to residential property but based on a still I captured from the scene where everyone is racing out the house, you can see that 8 year old Kieran Culkin is approximately the same height as the bannister plus the height of a staircase step. Using this I chose to approximate the bannister height as 36 inches. The last bit of data I needed was Joe Pesci’s height which I found to be 5 feet 4 inches.
When I plugged the dimensions listed into the equation previously formulated I was able to calculate the pendulum arm length as 56.75 inches or 1.44 meters.
The depiction of the pendulum is below with the arm length denoted by the letter “H”.
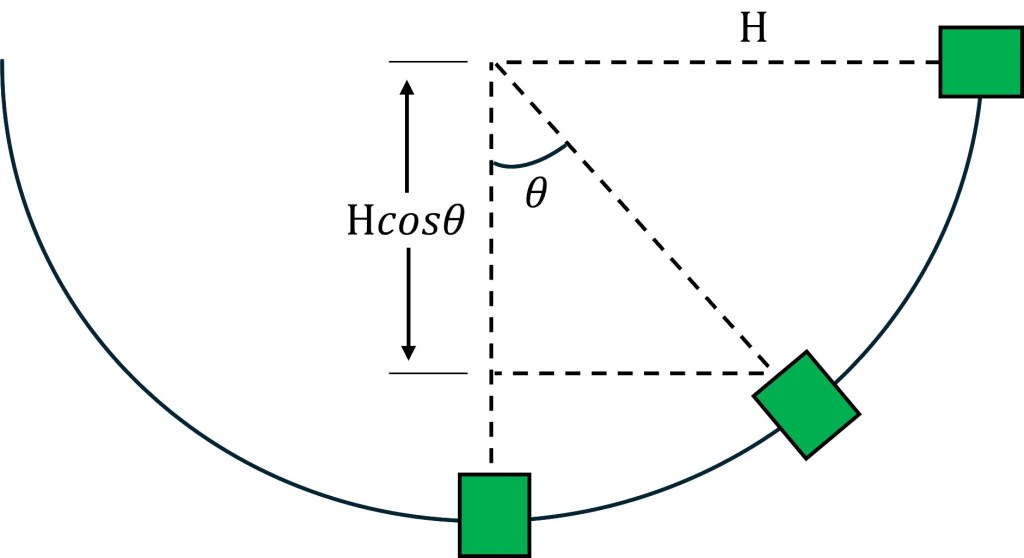
Due to the conservation of energy and ignoring air resistance, the energy of the paint can remains constant. The initial energy of the can is thus equal to the energy of the can at whichever arbitrary secondary point we pick.
Given that the energy of the paint can is a sum of both potential energy from height and kinetic energy (there are no other relevant energy sources to be considered here), I was able to derive the following equations.
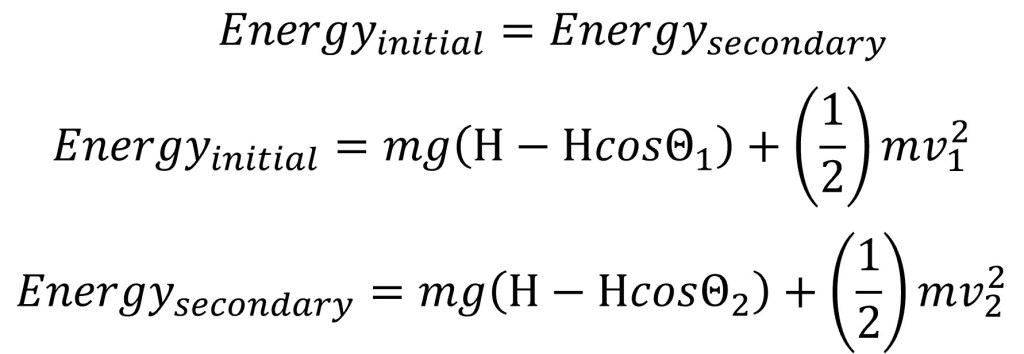
To make the calculations easier I chose to make the initial point the moment the paint can is fully extended from the bannister right before it begins to start its downward swing. This means that the kinetic energy is zero and the angle theta is 90 degrees. This eliminated two terms from the initial energy equation.
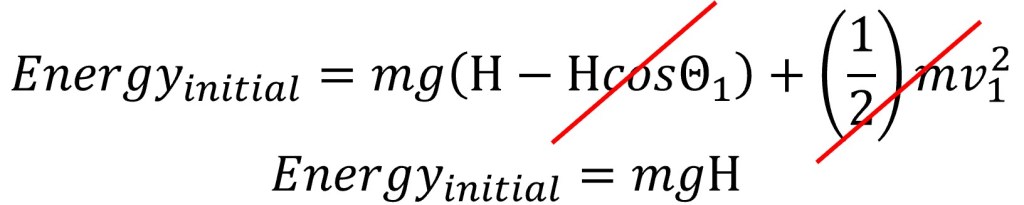
By setting the initial energy equal to the secondary energy equation and simplifying I was able to formulate the following and solve for the velocity at the secondary point.
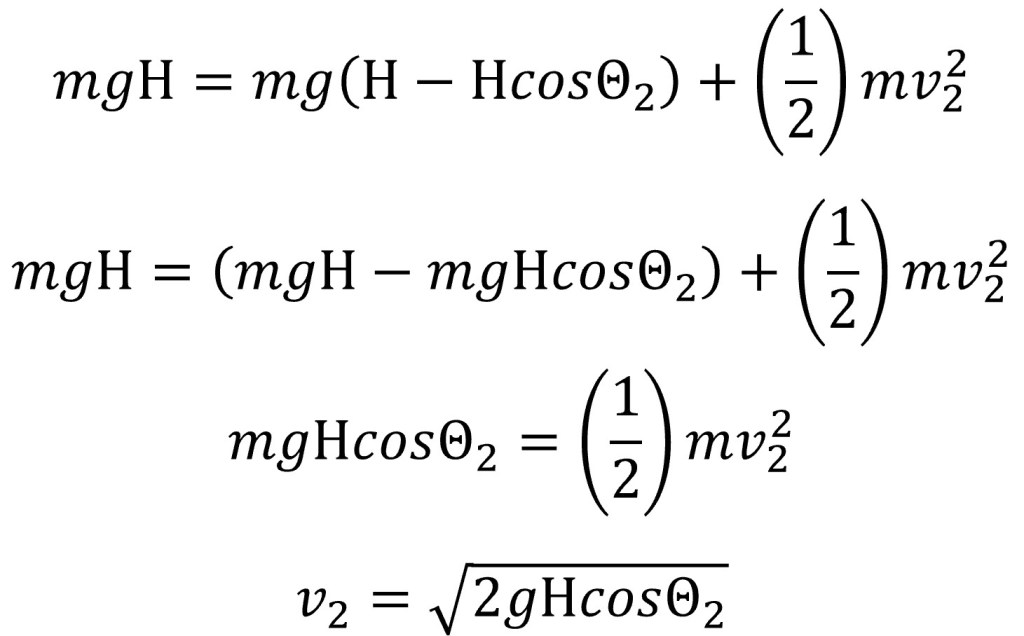
The paint can impacts Harry when it is at the bottom of the pendulum where the angle Θ is 0. Cos(0) is equal to 1 and due to this the velocity the can strikes Harry can be described as the square root of two times the acceleration of gravity times the pendulum length.
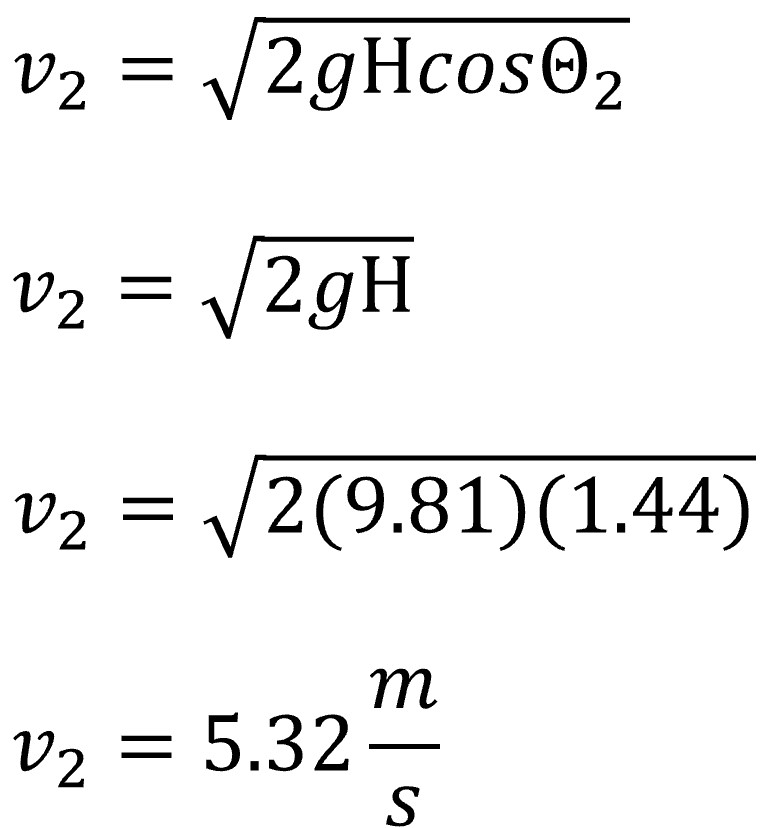
Plugging in the known values it was possible to solve for velocity, which was calculated as 5.32 meters per second.
The paint cans that struck Harry and Marv looked to be galloon paint cans; however, they did look used as there was paint dripping from the sides. The average weight of a galloon paint can is approximately 11 pounds or 4.99 kg. Assuming the paint cans are half full the momentum imparted on Harry from this impact would be 13.27 (kg⋅m/s). It wouldnt be impossible to believe that even if the cans were initially half full Kevin made sure to fill them up before using them. In that case the cans would have a momentum of 26.54 (kg⋅m/s) at the moment of impact. For reference, the average swing velocity of MLB batters (32.19 m/s) and the average bat weight (33oz or 0.94kg) results in momentum of 30.1(kg⋅m/s). If the MLB batter swung the bat 10 mph slower at a speed of 62 mph or 27.72 m/s, the momentum would equal 25.92 (kg⋅m/s). Essentially getting hit by full paint cans traveling at the speed seen in Home Alone is akin to being hit by a slow swinging MLB batter. These values are summarized in the table below.

While the momentum from the half-full paint can is only about half that from a slow MLB batter, I still do not believe Harry and Marv would walk away from such an impact with only a missing tooth. If the paint cans were full, well… I don’t think they would experience another Christmas.
I think it’s safe to say that the moral of all these physics calculations is to stay away from homes defended by psychopaths named Kevin.
Sources:
[1] Petriello, Mike. “Everything to Know about Statcast’s New Bat-Tracking Data.” MLB.Com, MLB, 16 May 2024, http://www.mlb.com/news/what-you-need-to-know-about-statcast-bat-tracking#:~:text=The%20average%20swing%20is%2072%20mph%2C%20and,something%20like%20Ke’Bryan%20Hayes%20or%20Edouard%20Julien.
[2] “Do Professional Players Use Heavy or Light Bats?” X Bats, X Bats, 1 Jan. 2014, http://www.xbats.com/blog/do-professional-players-use-heavy-light-bats.htm#:~:text=Most%20of%20today’s%20major%20league%20players%20typically,cannot%20make%20a%20wood%20bat%20this%20light).