Several months ago I was presented with a puzzle involving numbers and operators. The puzzle was to create five equations using the numbers 1-10 and each of the numerical operators. Each number from 1-10 has to be used once and only once. Each operator is to be used once and one operator can be used twice. The results of the five equations are 1, 2, 3, 4, and 5.
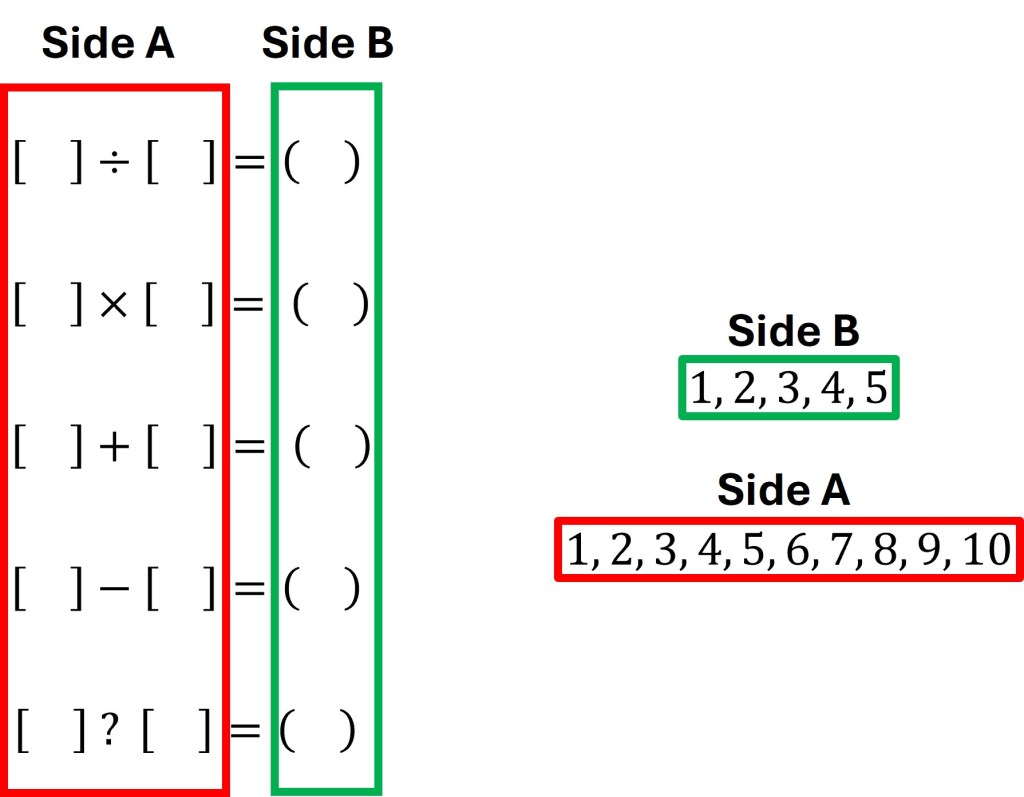
This puzzle took me a solid couple hours to initially solve and I recently decided to attempt it again and upon its completion to write about it. At initial glance the puzzle appears to be only solvable through brute force and trial and error. While trial and error may work in finding the solution, it is without doubt that this method would be terribly time consuming.
For anyone reading this who wants to try their hand at solving the puzzle free of spoilers, now is the time to stop and give it a whirl. Beware, past the below image will be the solution to this task.

Let’s start by exploring the equation that will use the multiplication sign. What two numbers from Side A when multiplied will result in a number between 1-5? If we initially exclude using the number 1, the only two numbers that could have a product between 1-5 are 2 and 2. However, we can’t use 2 twice. Each number can only be used once. Given this we now know that the number 1 has to be used with the multiplication sign and that the resulting product will also be one of the numbers multiplied. The only number the product can not be is 1 because that would necessitate the number 1 in Side A being used twice.
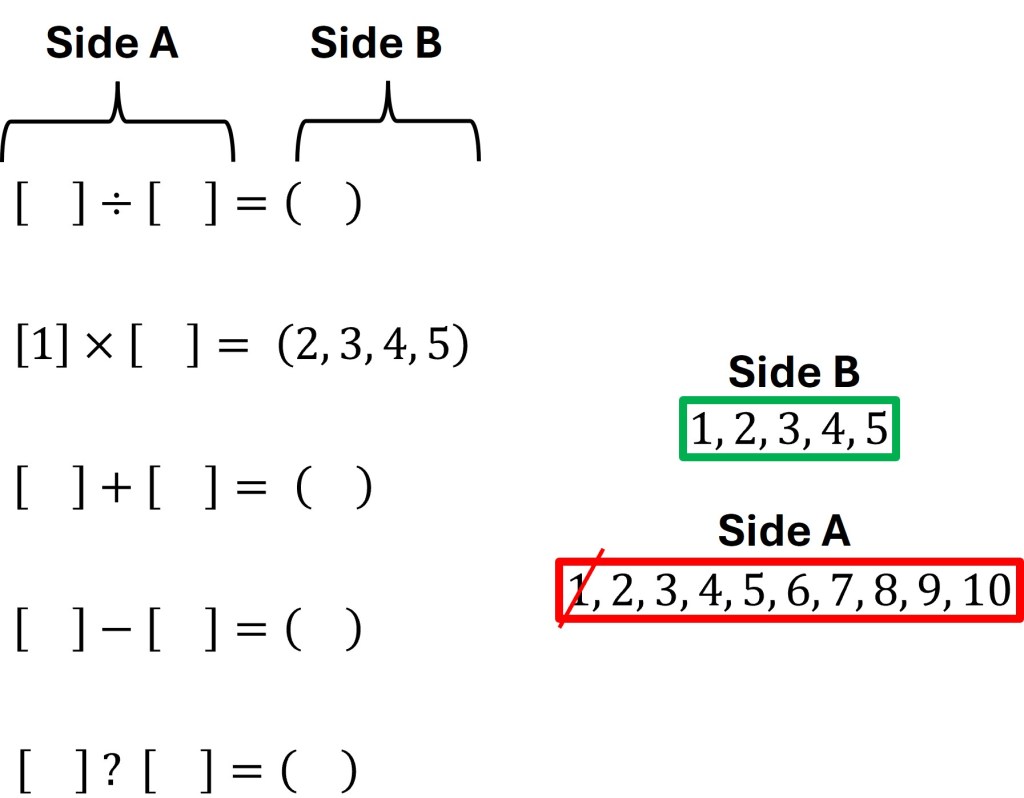
Now let’s explore a different operator; addition. Since the number 1 from Side A has been used, only 2 and 3 exist that can be used with addition to create a number from Side B. This means one of the equations has to be the sum of 2 and 3 equaling 5.
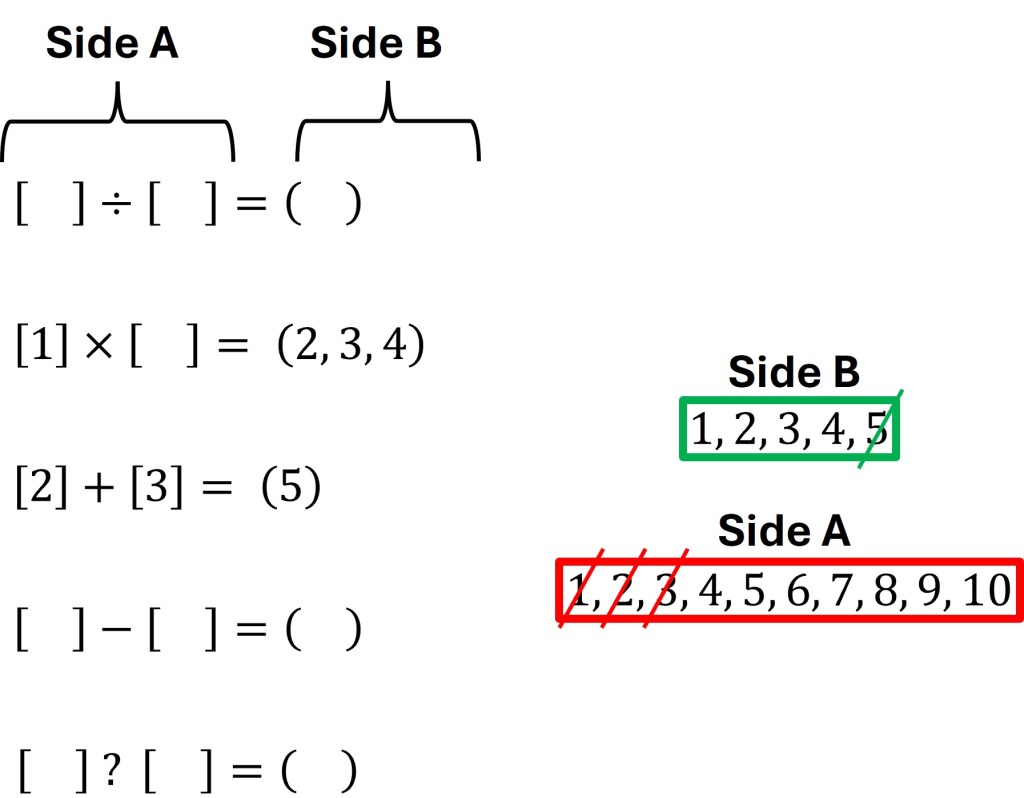
Our revelations from addition doesn’t stop here though. Due to the unique nature of using the number 1 with the multiplication operator, we know that whatever number we use in conjunction from Side A with 1 will also be the product of these two numbers. We have already used the numbers 2 and 3 from side A and the product of multiplication can not be 5 since that is the solution to our addition equation. Therefore the only number we can feasibly use in multiplication with 1 is 4.
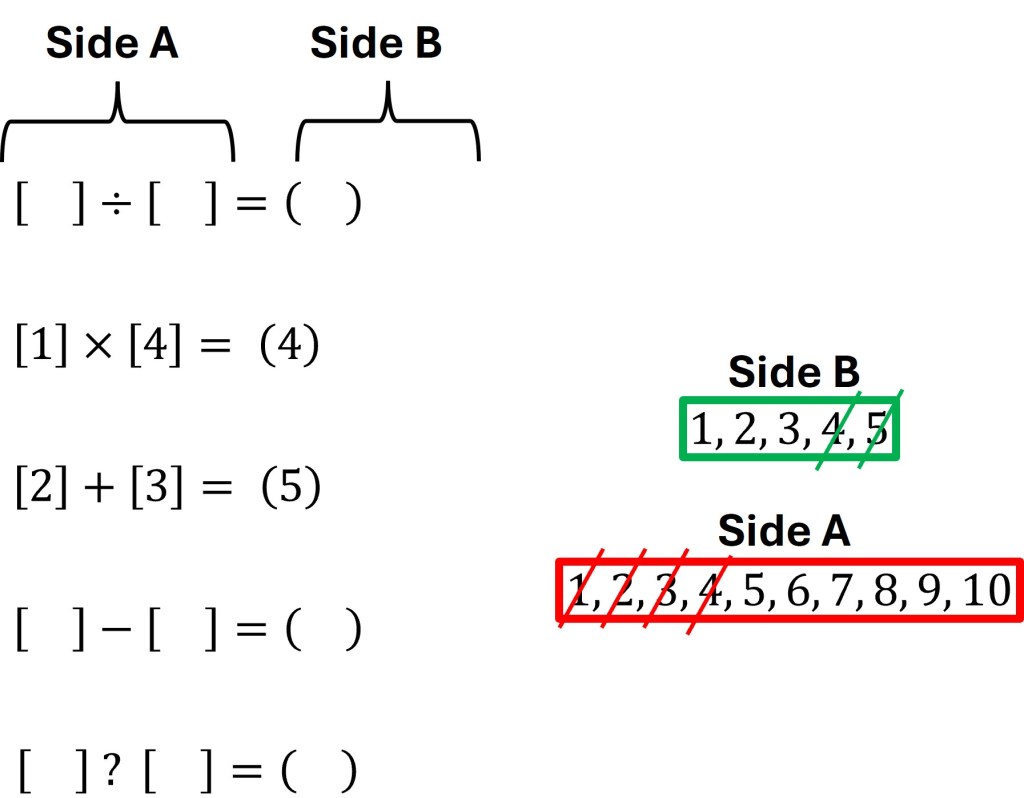
The next avenue to explore with this puzzle is division. Which numbers left from Side A when divided can result in a number from Side B? The answer here is much more obvious than the previous parts of the puzzle as 10 and 5 are the only two numbers left that fulfill this requirement.
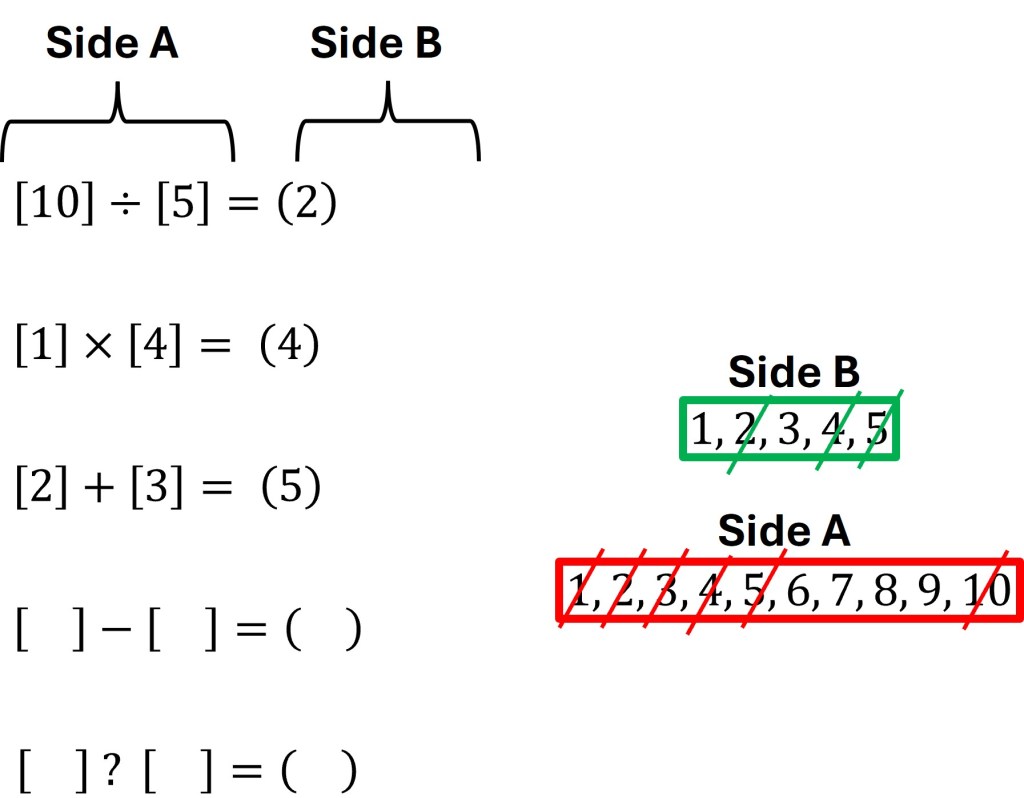
The two numbers left form Side B are 1 and 3. The numbers 6, 7, 8, and 9 remain from Side A. The remaining operators are subtraction and the mystery operator that can be any of the four operators. Examining this critically we know that the mystery operator must also be subtraction as there is no other way to use the remaining numbers from Side A to arrive at a number remaining from Side B.
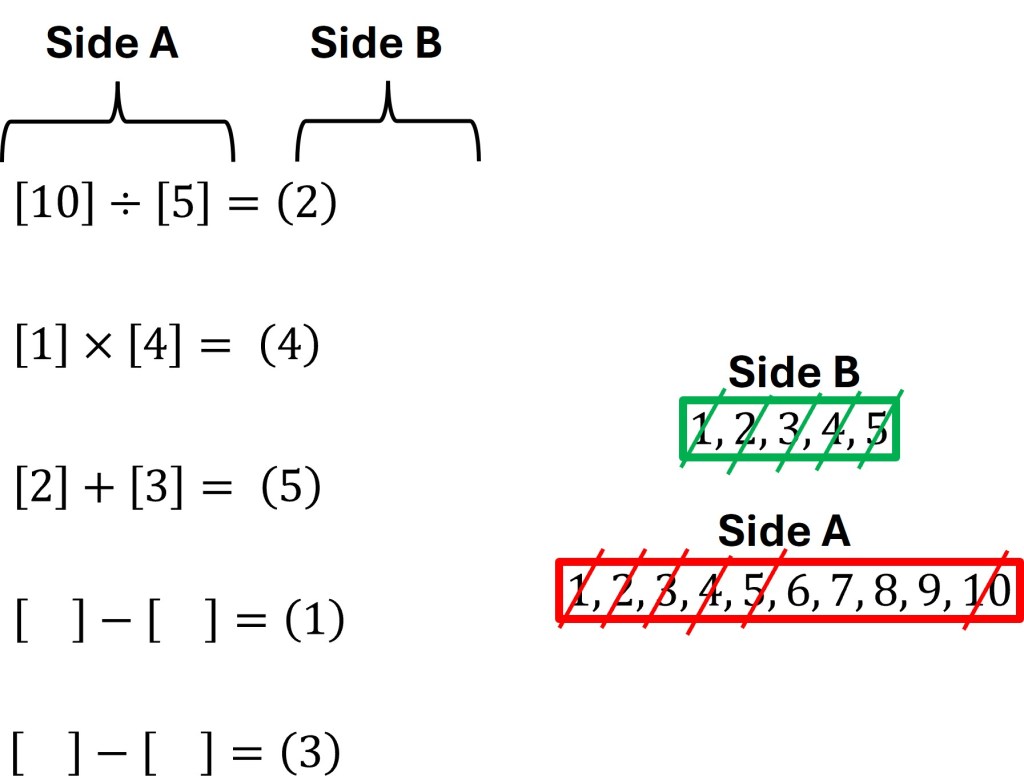
Four numbers remain from Side A to be used in two subtraction equations. Only two of the four numbers have a difference equating to 3: 9 and 6. That leaves 7 to be subtracted from 8 to yield 1. And thus the solution to the number puzzle is the following.
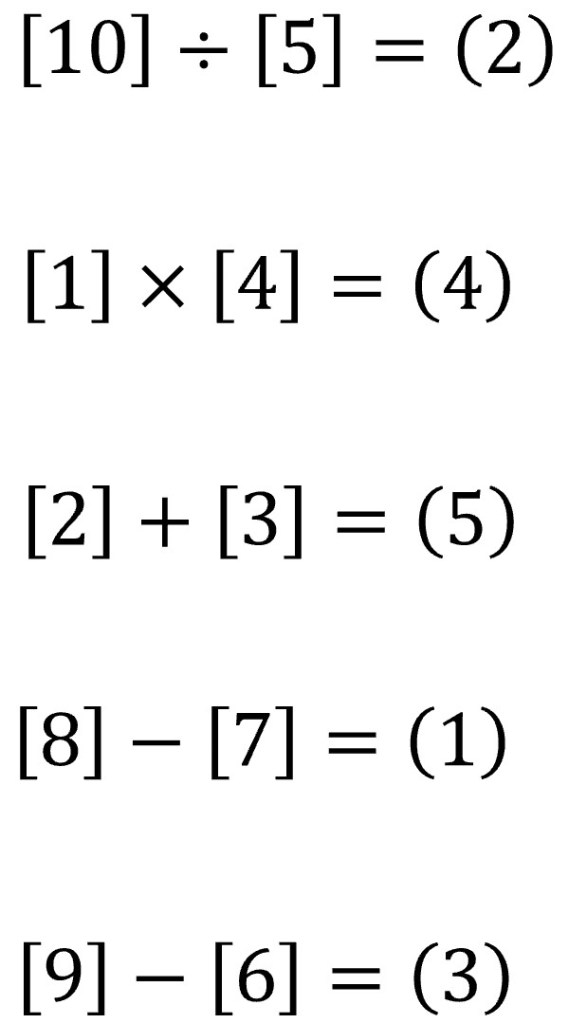
The solution to the math puzzle was solvable by picking apart the problem to find unique facets and exploiting these areas to whittle down the seemingly endless possible solutions until only one solution set remained.