Mindlessly scrolling through Reddit recently led me to a posting about finding the volume of an ingot shape. Many of the comments for this math question involved the clever prospect of using water displacement similar to the famous story of Archimedes discovering a method of calculating the volume of an oddly shaped crown. While this would lead to the correct calculation, it isn’t useful if we don’t have access to a properly dimensioned replica.
A depiction of the ingot and its dimensions can be seen below.

Not immediately noticing the fact that the bottom and upper lengths of the ingot (51.5 cm and 48 cm respectively) were unequal, I figured the problem was a simple one and that the solution was to find the area of the end trapezoid and multiply by the length of 51.5 cm to find the volume. Rereading the dimensions dispelled me of this solution and I quickly moved on to wondering if the volume could be solved by calculating the volume of a 13.5 x 8.0 x 51.5 cm rectangular prism and subtracting the necessary volume. This I also quickly discarded as I realized that if I used neat triangular prisms, I would be undercalculating the ingot volume as I would be subtracting more volume than necessary due to the overlap of the triangular prisms.
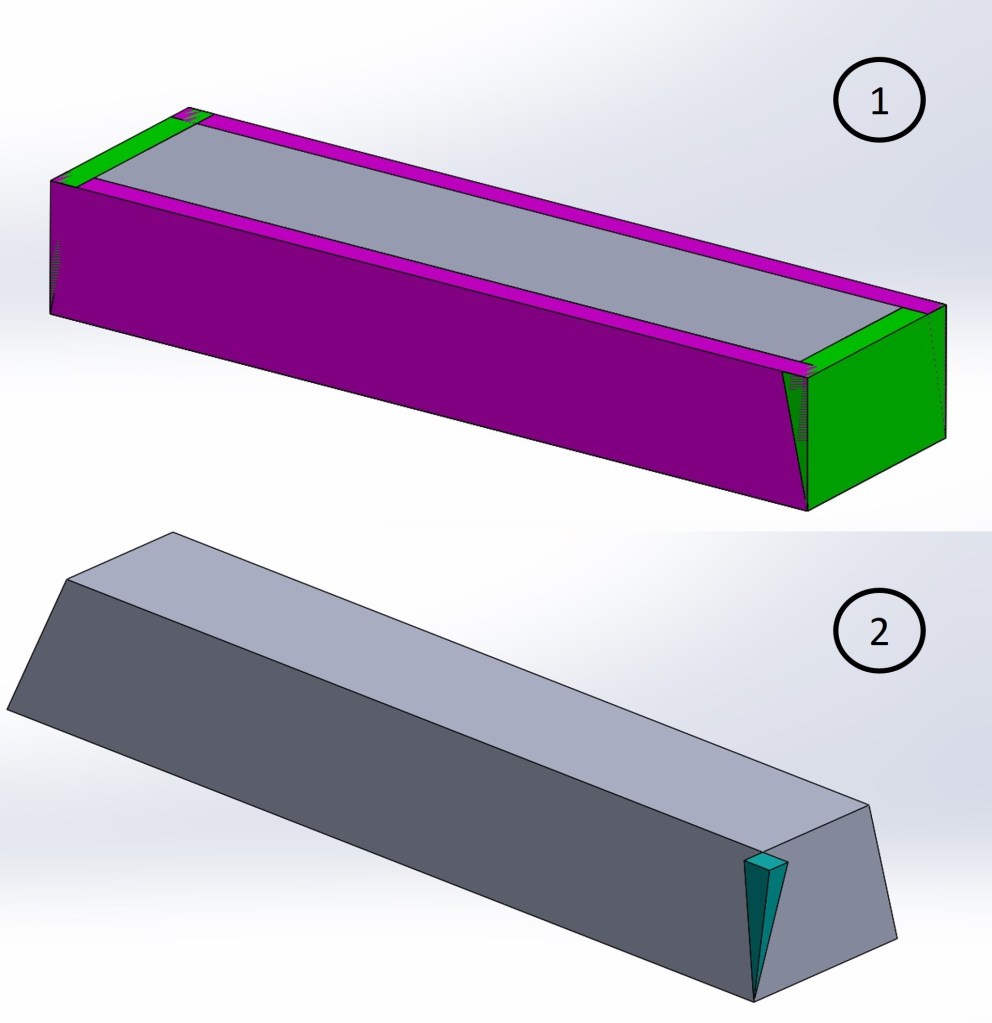
The volume of a rectangular prism 13.5 x 8.0 x 51.5 cm in measurement is 5562 cubic centimeters. If the necessary four triangular prism volumes (Fig. 2) were subtracted from this, the result would be 4652 cubic centimeters.
Since I modeled these shapes in SolidWorks I was able to use SolidWorks’ mass properties feature and find the exact volume of the ingot to be 4684.67 cubic centimeters. This shows that whittling away at a rectangular prism by way of triangular prisms as a way of determining the volume leads to the ingot volume being undercalculated by 32.67 cubic centimeters. The volume of the overlap portion at one corner of the ingot was calculated by SolidWorks to be 8.17 cubic centimeters. This makes sense as the undercalculated volume is equal to four overlap corner volumes after accounting for rounding error.
Creating prisms to subtract where there was no overlap created the same issue as solving for the ingot volume outright. The shapes necessary in this case wouldn’t have equal cross section area along a plane direction.
Thus I arrived at my third potential method for determining the volume of the ingot: integration. Being several years out of the classroom my integration skills were gathering dust inside my brain; however, I set about to take these skills out to prove to myself that I could still weld them and in doing so solve the volume question that had consumed my evening.
The first step was to determine the area I would integrate with respect to the x-direction (height of the ingot). The shape of this area is a rectangle and can be seen in the following image.
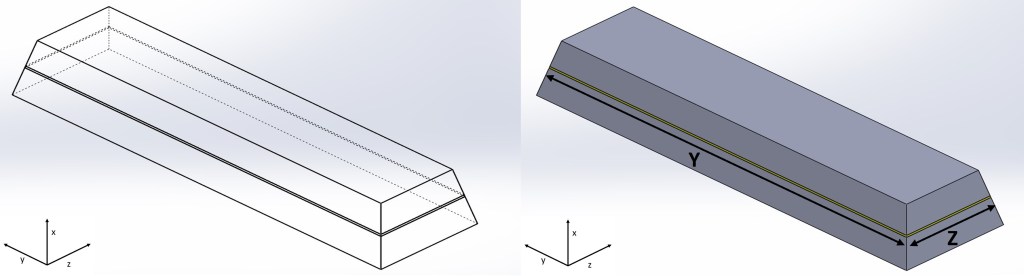
In order integrate the cross section area and find the ingot volume, the sides of the dimensions Y and Z (sides of the rectangular cross section) must be expressed in terms of x. Another way to say this is that the formula for the cross section area must be written in a way so that it can be calculated as long as the x-value is known and entered into the formula.
See the following image (Fig. 4) for how the dimension Z can be expressed in terms of the height, x.
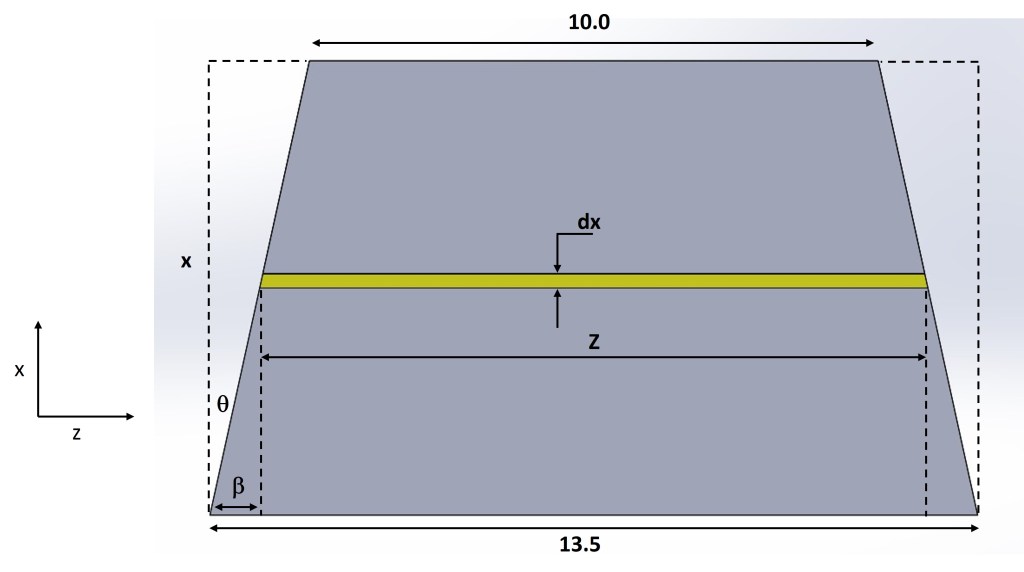
Since we know that the maximum value of β is 1.75 (we can find this by dividing the difference of the top and bottom trapezoid sides by two) and the maximum value of x is 8, we can use inverse tangent to calculate the angle of theta to be approximately 12.34 degrees. Creating an expression for Z that includes x demands us to use one of the known lengths of Z (either the min or max) and the length of the dimension β. This is done in the following series of equations.
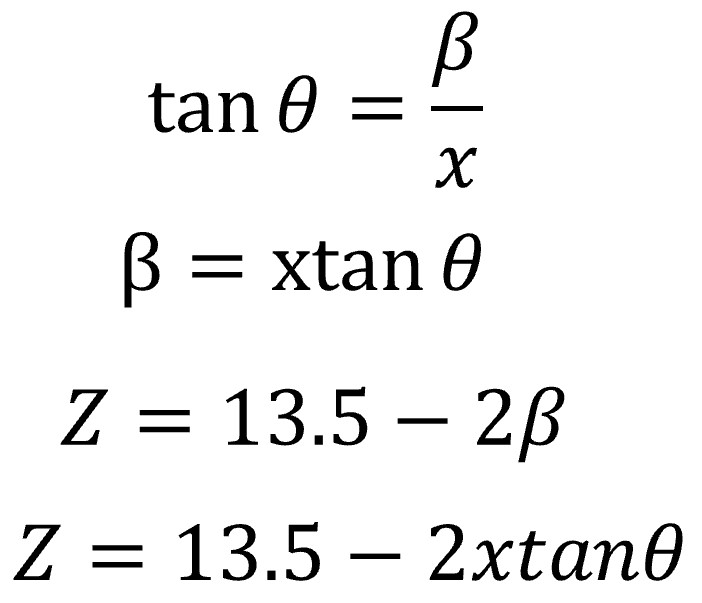
See the following image (Fig. 5) for how the dimension Y can be expressed in terms of the height, x.
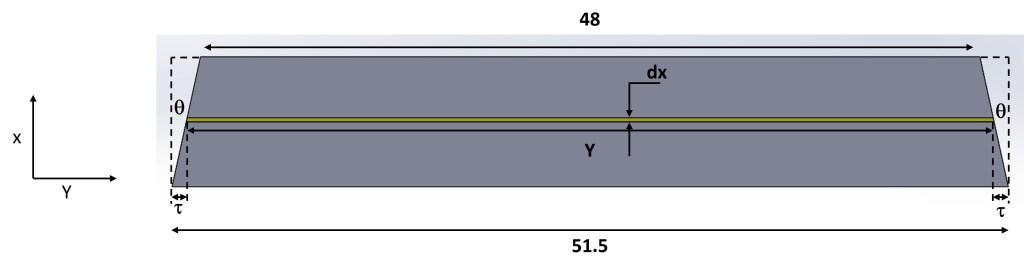
The sides of the triangle used to create the angle θ are also 8 and 1.75 centimeters in length and therefore the value for θ in this plane (x-y) is equal to the value for θ on the x-z plane seen in Figure 4. All the sides of the ingot have the same slope. The method to express Y in terms of x can be completed in a similar manner to how Z was expressed in terms of x. Instead of using the dimension β, τ will be used. This is done in the following series of equations.
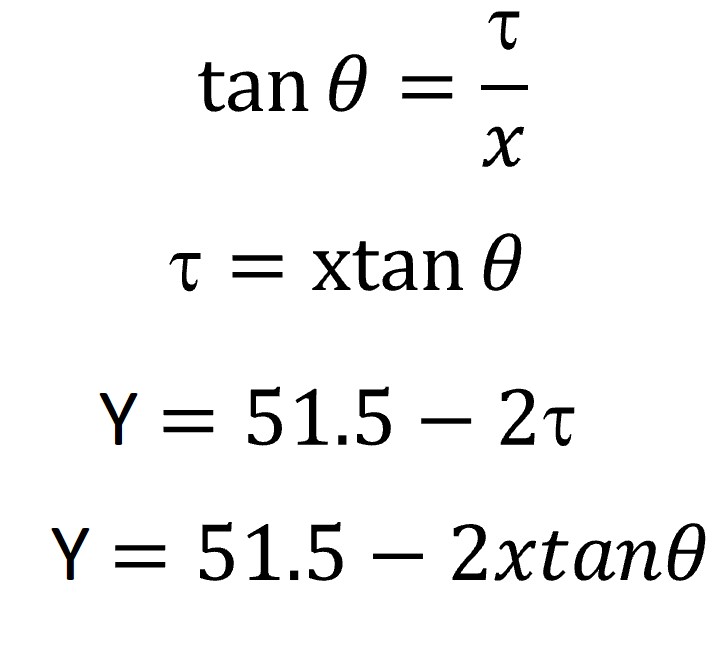
Since we now are able to express both Z and Y in terms of x, we can write the equation for the cross section area (along the y-z plane). Multiplying this area by dx (the infinitesimal height of the cross section, gives us the volume of the cross section. Then all that’s needed is for the definite integral with respect to x from 0 to 8 be taken of the cross section volume. This work is completed in the following steps/equations.

Taking the steps defined above and using 12.34 degrees as θ, the volume was calculated to be approximately 4683.70 cubic centimeters. The exact volume of the ingot was calculated by SolidWorks to be 4684.67 cubic centimeters. The value obtained through integration is only 0.021 percent off from the actual volume. The error is a result of the approximation done when taking the inverse tangent of θ.
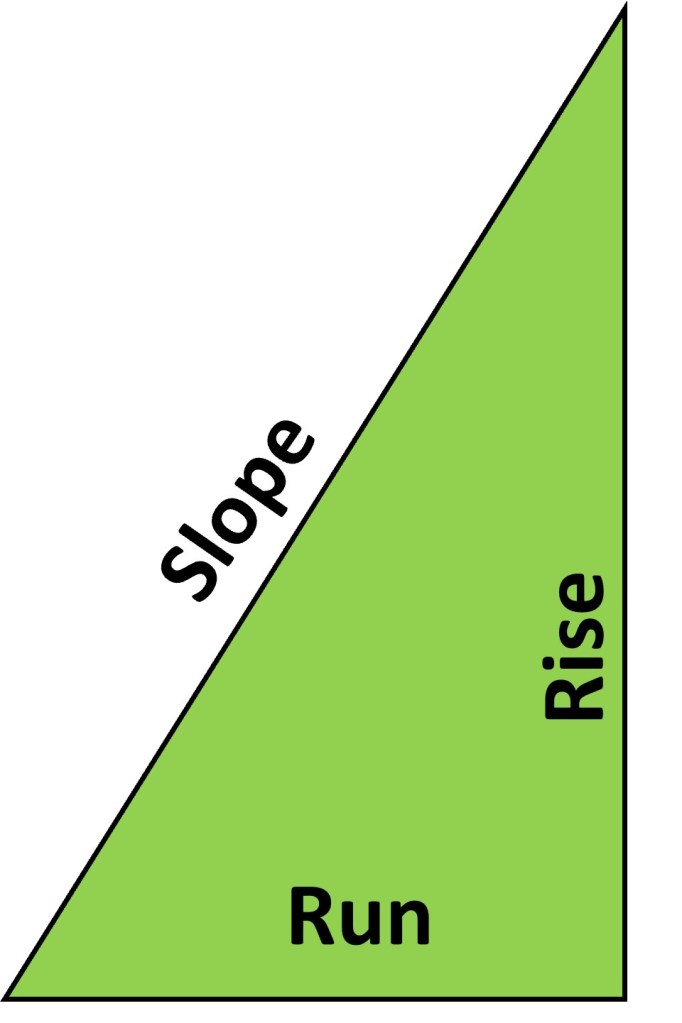
The exact volume can be found by directly using the inverse tangent of θ and not rounding until the very end of the calculations. It’s also possible to get the exact volume by utilizing the slope of the ingot faces and converting the tangent value into a fraction. The slope of an ingot face is equal to the rise over run. This can be calculated with the maximum rise of 8 cm and the maximum run of 1.75 centimeters. The slope is consistent all the way up the face of the ingot and therefore the value of 1.75 divided by 8 will equal the value of rise (x) over run (either β or τ). These calculations can be seen below Figure 6.
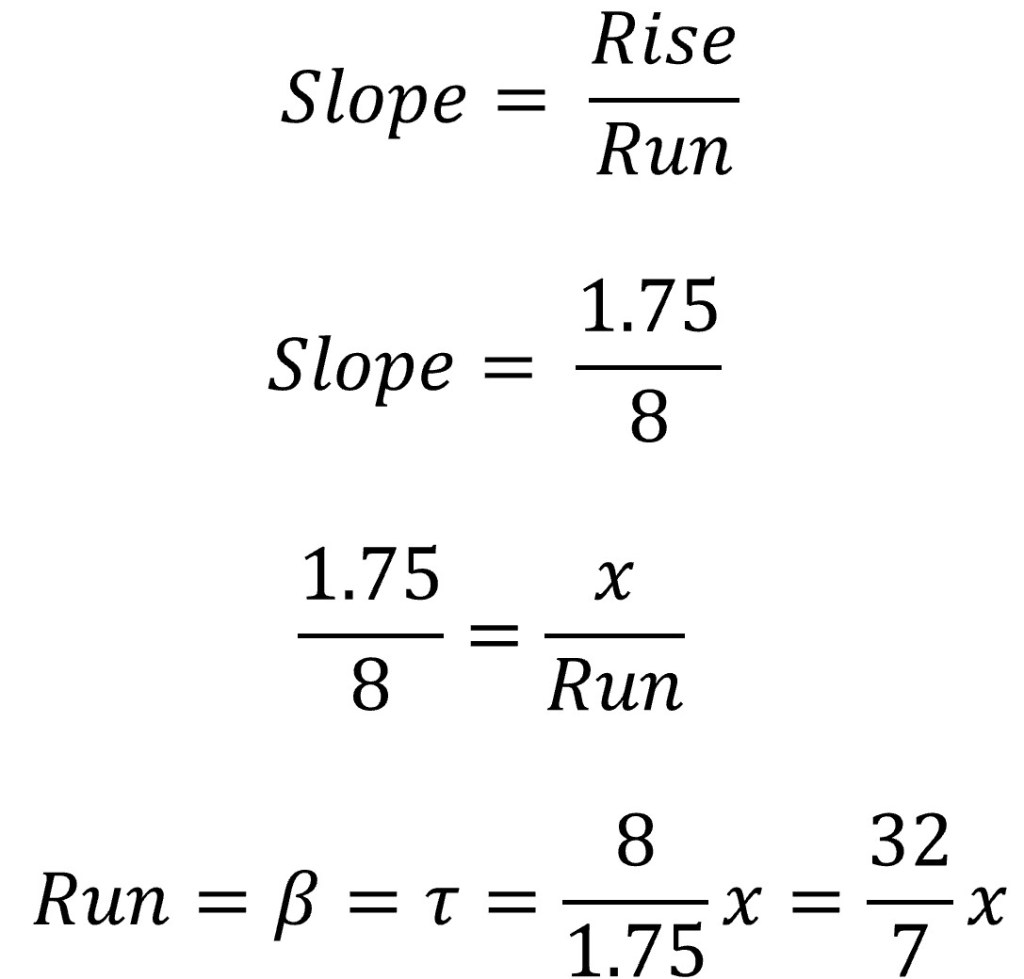
Using fractions in the equations for β or τ could allow for one to find the exact volume of the ingot as long as the fractions remained fractions until the very end. This may also be the way others first solved the problem; however, my mind went defaulted to calculating angles first as the angles in the geometry are often more useful than the slope of a face in my opinion.
Solving for the ingot volume was an unplanned quest that consumed my evening. However, becoming consumed in a challenging math problem, or perhaps more accurately a math problem that was challenging due to years of rust buildup on my math skills, is a thrill I have missed. I look forward to perusing Reddit for more math related side quests.